Overview

I2-NeRF is a physically grounded NeRF framework designed for media-degraded environments such as underwater, haze, and low-light scenes. The method combines:

• A general radiative formulation that unifies emission, absorption, and scattering under the Beer–Lambert law, covering various media types.
• A media-aware sampling strategy that allocates samples both on object surfaces and in low-density volumes, avoiding severe undersampling of the medium itself.
• Metric, isotropic perception enabled by explicitly modeling downwelling attenuation, so that the reconstructed field is consistent across directions once a global scale is known.

Abstract

we propose I2-NeRF, a novel neural radiance field framework that enhances isometric and isotropic metric perception under media degradation. While existing NeRF models predominantly rely on object-centric sampling, I2-NeRF introduces a reverse-stratified upsampling strategy to achieve near-uniform sampling across 3D space, thereby preserving isometry. We further present a general radiative formulation for media degradation that unifies emission, absorption, and scattering into a particle model governed by the Beer–Lambert attenuation law. By composing the direct and media-induced in-scatter radiance, this formulation extends naturally to complex media environments such as underwater, haze, and even low-light scenes. By treating light propagation uniformly in both vertical and horizontal directions, I2-NeRF enables isotropic metric perception and can even estimate medium properties such as water depth. Experiments on real-world datasets demonstrate that our method significantly improves both reconstruction fidelity and physical plausibility compared to existing approaches.

A Unified Model For Various Degradation Scenarios

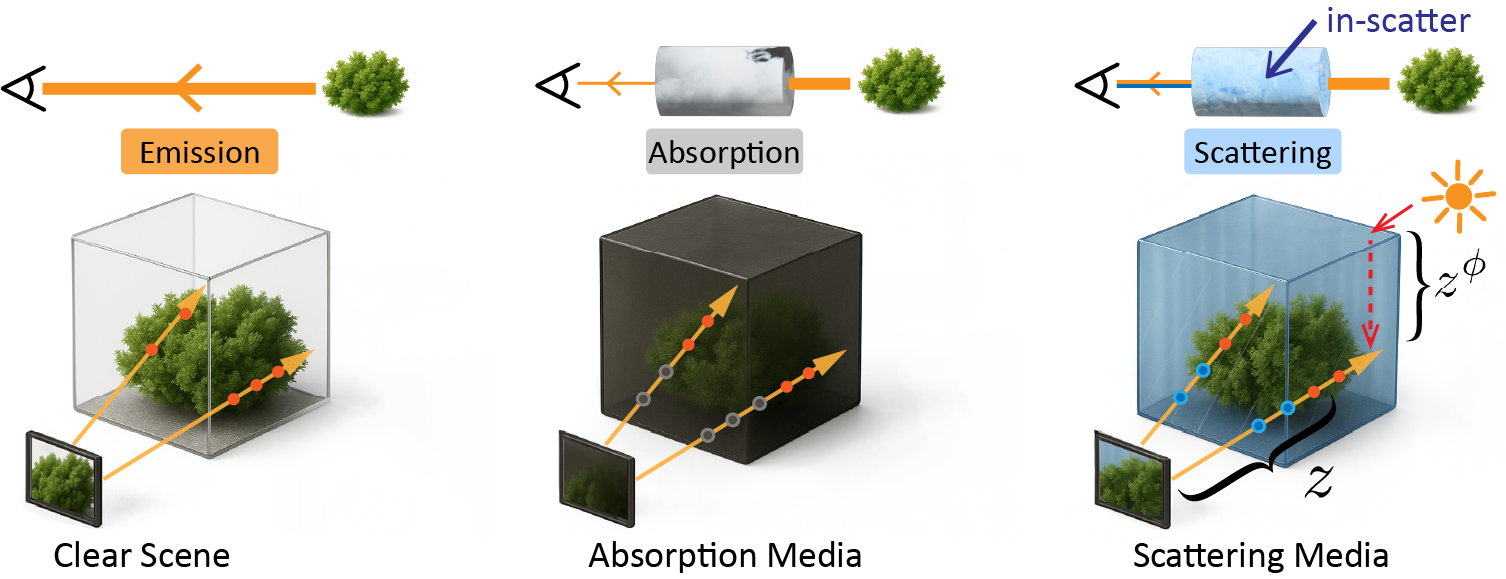
We unify degradations with one radiative formulation: Observation = Emission × Absorption + Scattering.

\( I \;=\; T\,J \;+\; \int_{0}^{z} T(0,t)\,S(t)\,dt \;\;\approx\;\; T\,J \;+\; (1-T)\,B \), with transmittance \( T=\exp(-\sigma\,z) \).

• Underwater. Wavelength-dependent extinction and backscatter: \( I(\lambda)=J(\lambda)\,e^{-\sigma(\lambda)z} \;+\; B_{\infty}(\lambda)\,\bigl(1-e^{-\sigma(\lambda)z}\bigr) \).
• Haze. Single extinction \( \sigma \) with air-light: \( I = J\,e^{-\sigma z} \;+\; A\,(1-e^{-\sigma z}) \).
• Low-light. Modeled as a virtual absorption field with negligible in-scatter: \( I \approx J\,e^{-\sigma z} \).

General Radiative Formulation

We decompose a camera ray into Emission (scene radiance \(J\)), Absorption (Beer–Lambert transmittance \(T\)), and Scattering (isotropic in-scatter). We also model downwelling attenuation with vertical light traveling distance, so the illumination that feeds the in-scatter decays as \(L_{\downarrow}(h)=\Phi\,e^{-\sigma z^{\Phi}}\). This keeps propagation consistent along the view direction and height, enabling isotropic, metric-faithful reconstruction.

Experimental Results

Lowlight Condition

Water Scattering Condition

Poster

Click the poster to view it in full resolution.

BibTeX

@inproceedings{liu2025i2nerf,
  title     = {I2-NeRF: Learning Neural Radiance Fields Under Physically-Grounded Media Interactions},
  author    = {Liu, Shuhong and Gu, Lin and Cui, Ziteng and Chu, Xuangeng and Harada, Tatsuya},
  booktitle = {Advances in Neural Information Processing Systems (NeurIPS)},
  year      = {2025},
}